问：

我在波士顿大学，最近在学MA575，老师可以帮忙梳理这门课的主要内容吗？因为我刚开始学就稍微有点跟不上，所以想找老师再补习一下。

答：

波士顿大学的数学课程MA 575（线性模型）为线性回归建模提供了进阶视角，内容涵盖：单变量与多变量线性回归；含多项式或因子回归；方差分析；加权与广义最小二乘法；变量转换；回归诊断；变量选择及线性模型的扩展。尽管部分内容可能在之前的基础课程中出现过，但MA 575旨在通过融入概率论与数学方法，深化对线性回归建模实践的理解。以下是对课程主要内容的梳理。

一、课程主题概要

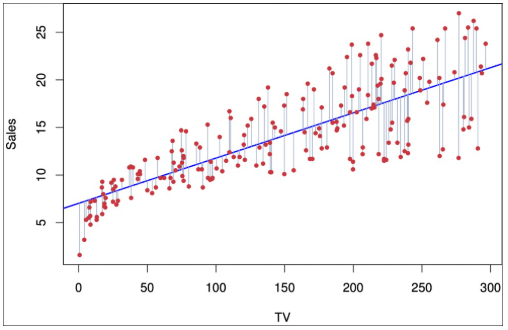
• 简单线性回归

• 诊断分析；变量转换

• 加权最小二乘法

• 多元线性回归

• 广义最小二乘法

• 时间序列分析

• 变量选择

• 选择后推断

• 预测评估

• RIDGE、LASSO等方法；

• 暂定主题：数据科学

二、主要内容解读

1、线性模型的理论框架

在导论阶段，课程会涉及：

- 线性模型的基本形式与假设条件（如线性性、独立性、方差齐性等）；

- 线性模型与统计推断的关系；

- 线性模型在社会科学、经济学、生物统计与机器学习中的应用场景；

- 对线性模型矩阵表示的初步介绍。

这一部分虽然看似基础，却是理解后续复杂模型的理论基石。

2、简单线性回归

在这一阶段，课程强调以下几个核心技能：

- 估计与推断：理解估计值的期望与方差、估计的无偏性与有效性。

- 模型拟合与可视化：利用残差图直观判断模型拟合质量。

- 假设检验：通过t检验与F检验评估模型参数是否显著。

- 预测与置信区间：区分个体预测与均值预测的不确定性来源。

这一部分的学习目标是让学生能够熟练掌握一元回归的数学原理与统计解释，并为多元回归建立直觉。

3、模型诊断与变换

学生将系统学习如何通过残差分析、标准化残差、Cook’s Distance 等方法评估模型是否存在异常值或高影响点。与此同时，课程也会教授变量变换的技巧。

4、加权最小二乘法与广义最小二乘法

加权最小二乘法（WLS）通过对不同观测赋予不同权重，能够在异方差存在时提高估计效率。

广义最小二乘法（GLS）更进一步，能够处理误差项间存在相关性的情况，如时间序列或空间数据中的自相关问题。

5、多元线性回归

在MA 575中，学生需要掌握以下关键内容：

- 模型的矩阵形式与正规方程求解；

- 多重共线性的识别与影响；

- 模型解释与偏回归系数的意义；

- 模型的整体显著性与单一变量显著性检验；

- 模型选择与拟合优度指标（如( R^2 )、调整后的( R^2 )）。

教师还会引导学生使用R或Python进行实际建模，让学生学会从数据预处理到模型评估的全流程分析。

6、变量选择与后选择推断

课程在这一部分深入探讨变量选择的策略，包括前向选择、后向剔除以及逐步回归等传统方法。MA 575还会介绍如何在选择模型后，仍能对参数进行有效推断，避免低估误差与过度自信的结论。

7、预测评估与模型比较

这一部分通常涵盖：

- 训练集与测试集划分的原则；

- 交叉验证（Cross-validation）与信息准则（如AIC、BIC）；

- 偏差-方差权衡的直观理解；

- 过拟合与欠拟合的识别与防范。

这部分训练让学生从“统计推断”走向“数据科学应用”，培养面向现实问题的建模思维。

8、RIDGE、LASSO等正则化方法

这部分将介绍岭回归（Ridge Regression）与LASSO等正则化方法。学生将理解这些方法在现代机器学习算法中的地位。

9、时间序列模型与广义回归框架

课程的后期还涉及时间序列分析的初步介绍。学生将学习如何处理观测间存在时间相关性的数据，理解自相关函数与模型拟合的调整思路。

这一部分并非完整的时间序列课程，但为学生提供了分析动态数据的入门视角。结合GLS的思想，学生将体会到线性模型如何自然延伸到更复杂的数据结构中。

10、数据科学主题

在这一部分中，学生会看到线性模型如何成为现代数据科学算法的理论基石。例如：

- 线性模型与广义线性模型（GLM）的衔接；

- 线性回归与机器学习算法（如随机森林、神经网络）的对比与联系；

- 模型可解释性与特征重要性分析；

- 数据清洗、特征工程与模型部署的流程化实践。

这一主题旨在让学生理解：传统统计理论并非过时，而是在现代数据分析框架中继续发挥核心作用。

总体而言，MA 575是一门兼具理论深度与实践广度的课程。通过学习，学生将能够建立扎实的建模思维，具备独立分析数据、评估模型、优化预测的综合能力，为后续在统计学、机器学习或数据科学等领域的深入研究打下坚实基础。

如果你在学习过程中遇到问题，可以立即联系考而思的课程顾问。考而思能够针对你的具体课业问题，提供一对一波士顿大学课程辅导。通过辅导，你将及时解决学习难点、巩固课程重点、消除知识短板、提升应用能力，从而获得满意的学业成绩。